I will suggest several tips, and discuss common beginner’s mistakes occuring when coding from scratch a Metropolis-Hastings algorithm. I am making this list from the top of my mind, so feel free to propose suggestions by commenting to this post. Most items are related to coding practice rather than actual statistical methodology, and are often not mentioned in widely available literature. If you are an instructor, you might find it useful to mention these issues in your class, to avoid students getting puzzled when coding mathematically flawless algorithms having a misbehaving implementation.
Notice, this post does not discuss the design of a Metropolis-Hastings sampler: that is important issues affecting MCMC, such as bad mixing of the chain, multimodality, or the construction of “ad hoc” proposal distributions are not considered.
I am assuming the reader already knows what a Metropolis-Hastings algorithm is, what it is useful for, and that she has already seen (and perhaps tried coding) some implementation of this algorithm. Even given this background knowledge, there are some subtleties that are good to know and that I will discuss below.
Briefly, what we wish to accomplish with Markov chain Monte Carlo (MCMC) is to sample (approximately) from a distribution having density or probability mass function . Here we focus on the Metropolis-Hastings algorithm (MH). In order to do so, assume that our Markov chain is currently in “state”
, and we wish to propose a move
. This move is generated from a proposal kernel
. We write the proposed value
as
. Then
is accepted with probability
or rejected with probability
where
Then is called acceptance probability.
A very simplified pseudo-algorithm for a single step of MH looks like:
proposeaccept
with probability
otherwise reject
However, since we wish to sample say times from
, we better store the result of our simulations into a matrix
and write (assuming an arbitrary initial state
)
for r = 1 to R proposecompute
accept
with probability
then store it into draws[r]:=
set
, set
otherwise store draws[r]:=
end
Here means “copy the value at the right-hand-side into the left-hand-side”. After a few (sometimes many) iterations the chain reaches stationarity, and its stationary distribution happens to have
as probability density (or probability mass function). In the end we will explore the content of
and disregard some of the initial values, to wash-away the influence of the arbitrary
.
1- You are given the pseudo-code above but it’s still unclear how to use it for sampling from 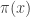
The very first time I heard of MH (self study and no guidance available) was in 2008. So I thought “ok let’s google some article!” and I recall that all resources I happened to screen were simply stating (just as I wrote above) “accept the move with probability and reject otherwise”. Now, if you are new to stochastic simulation the quoted sentence looks quite mysterious. The detail that was missing in my literature search was the logical link between the concept of acceptance probability and that of sampling.
Here is the link: you have to randomly decide between two possible outcomes of a random decision: accept or reject a move, and each of these two outcomes has its own probability ( for accepting and
for rejecting). So our decision is a random variable taking two possible values, hence is a Bernoulli random variable with “parameter”
. And here is the catch: to sample from a discrete distribution (like a Bernoulli distribution) you can use the inverse transform method, which in the special case of a binary decision translates to (i) sample a pseudo-random number
from a uniform distribution on the interval
, that is
which can be obtained in R via
, and (ii) if
accept
otherwise reject. That’s it (*).
(*) Well, yes that’s it. However the coding of the implementation can be simplified to be just: if then accept
otherwise reject it. This is because
hence whenever
is larger than 1, then certainly
.
In conclusion for a single MH step we substitute (and for simplicity here we remove the dependency on the iteration index we introduced in the previous code)
computeaccept
with probability
with
simulateif
then
and
2- Do not keep only the accepted draws!
A common mistake is not advancing the iteration counter until we have an accept. This is wrong (hence if you ever coded a MH algorithm using a loop it is fairly likely you may have acted the wrong way). In the implementation given in the introduction to this post (the one using the
loop) you may notice that when a proposal is rejected I store the last accepted value as
.
3- Save and reuse the values at the denominator
If you compare the pseudo-codes suggested above you may have noticed that when a proposal is accepted I “save” , in addition to storing the accepted proposal
. While it is not necessary to do the former (and in fact most descriptions of MH in the literature do not mention this part) it is a waste of computer time not to keep in memory the accepted
, so that we do not need to recompute it at the next iteration (since it is reused at the denominator of
).
This is especially relevant when MH is used for Bayesian inference, where is a posterior distribution
such that
for some “prior”
and “likelihood function”
. In fact, it is often the case that the pointwise evaluation of the likelihood is far from being instantaneous, e.g. because the data has thousands of values, or the evaluation of the likelihood itself requires some numerical approximation.
4- Code your calculations on the log-domain.
Depending on cases, may sometimes take very large or very small values. Such extremely large/small values may cause a numeric overflow or an underflow, that is your computing environment will be unable to represent these numbers correctly. For example a standard Gaussian density is strictly positive for all real
, but if you evaluate it at
your software will likely return zero (this is an underflow).
For example, in R type and you’ll see it returns zero .
Therefore instead of using
ifaccept
otherwise reject
use
ifaccept
otherwise reject
Anyhow, while this recommendation is valid, it might not be enough without further precautions, as described in the next point.
5- Do as many analytic calculations as feasible in order to prevent overflow/underflow.
Strongly connected to the previous point is coding without doing your calculations analytically first. That is, I see beginners trying to use the log-domain suggestion from point 4 to evaluate
. This will not help because the log will be applied to a function
that has already underflown, and the logarithm of zero is taken.
In R you can use to compute
which is the safe way to evaluate the (normalised) standard Gaussian log-density. For other languages you may need to code the log-density yourself.
However, since we are interested in using MH, we may even just code the unnormalised log-density
where I have omitted the irrelevant (for MH) normalization constant . This brings us to the next point.
6- Remove proportionality constants.
An important feature of MH is that it can sample from distributions that are known up to proportionality constants (these constants are terms independent of ). This means that
can be an unnormalised density (or an unnormalised probability mass function). As mentioned in the previous point, we do not strictly need to write
but can get rid of the normalization constant
that anyhow simplifies out when taking the ratio
.
The simplification of proportionality constants is not just a matter of coding elegance, but can affect the performance of the algorithm. For example if is a Gamma distribution, such as
then
contains Gamma functions
as part of the proportionality constant. When
is not an integer but is a positive real number the evaluation of
involves the numerical approximation of an integral. Now, this approximation is not honerous if executed only a few times. However, often MCMC algorithms are run for millions of iterations, and in such cases we can save computational time by removing constants we don’t need anyway. In conclusion, you can safely avoid coding
(or its logarithm) as it is independent of
.
7- Simplify out symmetric proposal functions
A symmetric proposal function is such that for every
and
. Therefore symmetric proposals do not need to be coded when evaluating the ratio in
as they simplify out.
For example, assume a multivariate Gaussian proposal function written as (with some abuse of notation) , that is a Gaussian density with mean
and covariance matrix
. Then we have
where denotes is the determinant of a matrix and
denotes transposition. Clearly this
is symmetric because of the quadratic form at the exponent.
8a- Remember the transformation Jacobians!
Most previous recommendations are related to numerical issues in the implementation of MH. However this one alerts you of an actual statistical mistake. I introduce the problem using a specific example.
A Gaussian proposal function is a simple choice that often works well in problems where
is low dimensional (e.g.
is a vector of length up to, say, five elements) and the geometry of
is not too complicated. The fact that a Gaussian proposal has support on the entire real space makes it a useful default choice. However, when some elements of
are constrained to “live” in a specific subset of the real space, we should be aware that a significant proportion of proposed values will be rejected (unless we “design”
to intelligently explore only a promising region of the space). Wasting computational time is not something we want right?
For the sake of illustration, let’s assume that is a positive scalar random variable (see point 8b below for a more general discussion). We could code a Metropolis random walk sampler with Gaussian innovations as
where the “step length” is chosen by the experimenter and
is sampled from a standard Gaussian. Therefore we have that
. Clearly
will certainly be rejected whenever
since we are assuming that the support of the targeted
is positive.
A simple workaround is to propose instead of
, that is code
for some other appropriate . Then we evaluate
as
, that is we exponentiate the proposal
before “submitting” it to
. Now if this is all we do, we have a problem.
Thing is we proposed from a Gaussian, and then we thought that exponentiating the proposal is just fine. It is almost fine, but we must realise that the exponential of a Gaussian draw is log-normal distributed and we must account for this fact in the acceptance ratio! In other words we sampled using a proposal function that here I denote
(which is Gaussian) and then by exponentiating we effectively sampled
from another proposal
(which is log-normal).
Therefore, from the definition of log-normal density we have (recall in this example
is scalar)
or equivalently .
Then we notice that this proposal function is not symmetric (see point 7) and . Hence the correct sampler does the following: simulate a
and using all the recommendations above we
and reject otherwise.
But how would we proceed if we were not given the information that the exponential of a Gaussian variable is a log-normal variable? A simple result on the transformation of random variables will assist us, when the transformation is an invertible function. Say that for a generic
we seek for the distribution of
, and using the transformation rule linked above we have that
has density function
. Notice here
is the “Jacobian of the transformation”.
Therefore, we should not forget the “Jacobians” when transforming the proposed draw. In our example above is
and the ratio
in the acceptance probability is the ratio of Jacobians.
8b- Recall the tranformation Jacobian! Part 2
The discussion in 8a above treats the specific case of using a random walk proposal to target a distribution with positive support. How about different type of constraints? My colleague at Lund University Johan Lindström has written a compact and useful reference table, listing common transformations of constrained proposals generated via random walk.
See also an excellent and detailed post by Darren Wilkinson.
9- Check the starting value of
Generally it is not really necessary to place checks for infelicities produced by the MCMC sampler in your code. That is, it is not necessary for each proposed to check for complex values or check that
does not result into a
(not-a-number) or that you do not get, say,
(yes these things can happen if you code
yourself without caution or when this is the result of some approximation, e.g. the expression for
is not analytically known).
In fact in these cases the uniform draw in point 1 above will not be considered as smaller than
. So the comparison
will evaluate to a logical
statement and the proposed
will be rejected, as it should be.
However an exception to the above is when we evaluate at the starting value
. In this case we do want to check that
is not something unwanted. For example, say that
(or
) and we just put this value at the denominator of the ratio in the definition of
(since this is the starting value it automatically goes into the denominator). Then at the first proposed
we have (assume
is finite)
Clearly no will ever be accepted, therefore the value of
at the denominator will stay
for all iterations and the sampler will never move away from
.

Pingback: Why and how pseudo-marginal MCMC work for exact Bayesian inference | Umberto Picchini's research blog
Thank you for the very useful post, especially 8a and 8b, this is while looking for info on this that I came here.
There is one point though that is not developed and that causes me trouble in the implementation:
Let’s assume like in the example that my proposal is a Normal with sd ‘sigma’ (represented by ‘delta’ in your example), and that I need the support to be on [a,b], so I apply the corresponding change of variables listed in the PDF sheet. Now I will draw my new variable with respect to a Normal still, but what should the sd of that Normal be? Because in your post you say “for some other appropriate ‘delta^\tilde’ ” but I have not found exactly how to define it yet.
LikeLike
Thanks!
\delta and \tilde{\delta} are tuning parameters, that have really nothing to do with the problem treated in 8a-8b- These are simply standard deviations for the proposal mechanism. If you have to hand-pick \tilde{\delta}, just set it small enough that the chain starts moving. There are not other theoretical issues you should be worried about. In fact, it will be the targeted distribution (equipped with the appropriate Jacobian) that will take care of rejecting proposals outside [a,b]. For example a post by Darren Wilkinson, shows how to target a positive distribution using a Gaussian proposal, see https://goo.gl/KDnsgK
More specifically. Standard deviations for proposal densities should either (i) be set by the statistician appropriately, if he/she knows something about the “scale” at which the targeted variable x varies and if the size (dimension) of x is not too large; or (ii) let the standard deviation of the proposal be updated according to some adaptive method. A simple and often effective scheme is https://projecteuclid.org/euclid.bj/1080222083 (the main algorithm is at the beginning, while the rest of the paper is about its theoretical validation).
So, all in all this is part of the design of an efficient MCMC algorithm that, as I explicitly stated, I wish to avoid discussing as it is problem dependent (“…, or the construction of “ad hoc” proposal distributions are not considered.”)
LikeLike
Thanks a lot for your reply!
I understand exactly what you are talking about because I have precisely implemented Haario’s AM, and I had read Darren Wilkinson’s post 🙂
The background is that I am doing parameter estimation with a model that is a black-box function that has no analytical form, I can just run it fast. I implemented MCMC with AM with a multivariate Gaussian proposal, and it works decently well.
But there are a couple variables that have a support on some [a,b], so I want to try what you wrote with the transformed variables ‘trick’ to improve the acceptance rate (instead of having many steps rejected since the likelihood will be bad, but it costs runs of the function, and so wastes computational time as you state).
My point is that during AM, at the covariance update step (I say covariance matrix for generality, since I assume the multivariate case here, as that’s what I work with, but it shouldn’t change from the 1D case), you have this simple recurrence formula that gives the new covariance of the ‘real’ parameters, not the transformed ones. But now with your scheme, if I understood correctly, I have to draw my new parameters in the ‘transformed space’ as a function of the current transformed parameters, and a certain covariance. And if I want to preserve the efficiency of AM, this covariance cannot be whichever one I want right? Doesn’t it have to be some function of the new one I just calculated? I just would like to know what is this ‘some function’ that gives the optimal covariance for the transformed parameters.
It is possible I misunderstood something, so to be extra clear (and I am sure it could serve someone else stumbling on this post), here is what I do now with standard MCMC with AM:
0) I have my current parameters X (here they can be in ]-Inf,+Inf[, but they actually should be in [a,b] for efficiency.)
1) I update Sigma, the covariance matrix, with the convenient recurrence formula of Haario
2) I draw X’ ~ Normal(X, Sigma)
3) I compute the new likelihood \pi(X’)
4) I check the acceptance by looking at \pi(X’) / \pi(X) (actually I do it with the log as you suggested 🙂 )
5) I update my chain with either X’ if there is acceptance, or X if not
Now with your scheme, if I understood correctly, the steps are as follows:
0) I have my current parameters X
1) I update Sigma, the covariance matrix, with the convenient recurrence formula of Haario
1′) I transform them: Y = g(X) = (b+a*exp(-x))/(1+np.exp(-x)) (note: working with exp(-x) is better than exp(x) for numerical purposes)
2) I draw Y’ ~ Normal(Y, Sigma’) <—– What is Sigma' ???
2') I compute X' = g^-1(Y') for point 4) and 5)
3) I compute the new likelihood \pi(Y')
4) I check the acceptance by looking at \pi(Y') / \pi(Y) * (X'-a)(b-X') / (X-a)(b-X)
5) I update my chain with either X' if there is acceptance, or X if not
So as you can see at 2) in the new scheme, I am stuck because I am not sure which sigma to use. I hope I made it clear enough, please don't hesitate to ask if it isn't 🙂
LikeLike
honestly, I would set the entire inference by proposing from the transformed parameter immediately, so that you do not compute S and then wonder what S’ should be like. For example, say that you have two parameters x1 and x2. Say that you want parameter x1 to be in [a,b] with a>0 and b>0, whereas x2 is defined on the entire real line. So X =(x1,x2). However set all your code to work with Y = (logx1,x2). So you propose Y’ ~ N(Y,Sigma) where Sigma is automatically updated via Haario’s. Then of course your model simulator/likelihood does not take logx1 as input, and instead wants x1. So take x1:=exp(logx1) before feeding it to the model. Then place a prior on x1 (not logx1), one that has support on [a,b] (truncated normal, uniform, whatever…), and finally multiply by the Jacobian J= x1*/x1_old. This way your prior takes care of the fact that x1 has to be in [a,b], while the Jacobian corrects for the fact that you propose logx1. In the end you will have a chain for logx1 and one for x2. Do you want to report posterior marginals for x1? Take the exponential of the produced chain.
Now, if this is still causing you troubles, meaning that way too many proposals are produced that end outside the bounds, and this is an issue because your simulator is toooo expensive, then I wonder whether there is actually a problem with your model representing your data well. Perhaps there is a modelling issue and your interaction between model and data suggests that areas outside of [a,b] are not implausible.
LikeLike
Thanks again for the reply!
Your suggestion makes a lot of sense and sounds easier to implement (though I would really like to know what Sigma’ to use, in a theoretical sense 🙂 ).
But there is one point that I do not understand in your scheme:
it seems to me that you propose twice x1, since you propose first Y’ = (log(x1′), x2′) ~ N(Y =(log(x1), x2), Sigma), and then you say to put a prior on x1′ (let’s say a Uniform(a,b)), so I don’t really understand how that would work in practice? Wouldn’t that cancel completely the proposal on log(x1′) if I put a Uniform(a,b) prior on x1′ independently of what I just got as a proposal from the Normal?
If I understand, you suggest:
0) Outside of the Metropolis loop, go from X = (x1, x2) to Y = (log(x1), x2)
In the Metropolis loop:
1) I have my current parameters Y
2) I update Sigma, the covariance matrix, with the convenient recurrence formula of Haario
3) I draw Y’ ~ Normal(Y, Sigma)
4) I take x1′ = exp(log(x1′))
5) x1′ ~ Uniform(a,b) <—- This destroys my proposed x1' that I just had?!
6) I compute the new likelihood \pi(x1’, x2')
7) I check the acceptance by looking at \pi(X’) / \pi(X) * X'/X
8) I update my chain with either Y’ if there is acceptance, or Y if not
As you can see, step 5 does not make a lot of sense to me, but I must have misunderstood something you said.
It seems to me that it would be even easier to use instead of log, the good function such that Y=(g^-1(x1) = log(x1-a)-log(b-x1), x2), outside the Metropolis loop (then x1=g(y1) is in [a,b]), and put the good Jacobian for the ratio…no?
LikeLike
yes the above is about correct (fixes are below), but first a comment regarding step 5: if with “x’~U(a,b)” you mean “I evaluate the prior U(x’;a,b)” (rather than “I sample x’ from U(a,b)”) then it is ok, and it is not that you are “destroying the proposed x1′”. We are free to propose parameters the way we prefer, in this case using a Gaussian, and then have whatever prior is sutable for our data-modelling problem. The proposal just (well) proposes values in a, hopefully, efficient way (the ideal would be to have a proposal very similar to the posterior target). But you can use whatever prior makes sense for your problem even if this is not the same as your proposal.
So, I think it should be:
0) Outside of the Metropolis loop, go from X = (x1, x2) to Y = (log(x1), x2)
In the Metropolis loop:
1) I have my current parameters Y
2) I update Sigma, the covariance matrix, with the convenient recurrence formula of Haario
3) I draw Y’ ~ Normal(Y, Sigma)
4) I take x1′ = exp(log(Y′))
5) compute the priors \pi(x1′) and \pi(x2′), where for x1’we have say \pi(x1′)=U(x1′;a,b)
6) I compute the new likelihood \pi(x1’, x2′)
7) I check the acceptance by looking at (pi(x1’, x2′)/pi(x1, x2)) * (pi(X’) / pi(X)) * X’/X
8) I update my chain with either Y’ if there is acceptance, or Y if not
LikeLike
also see the reply I sent to your Github email address a few days ago
LikeLike
Dear Professor Picchini:
Thanks for the post. Very useful.
However, there is one part of your reply to viiv of 2 October 2018 that is unclear to me.
Step 7 states “check the acceptance by looking at (pi(x1’, x2′)/pi(x1, x2)) * (pi(X’) / pi(X)) * X’/X.”
Is the last ratio, X’/X, element by element division or something else?
Best regards,
Jim
LikeLike
Hi Jim, yes it’s element-by-element division.
LikeLike
I think you mean the determinant of X’ divided by the determinant of X if they are multidimensional, no?
And in general: the determinant of g^-1(X) divided by the determinant of g^-1(X’), if you follow your PDF sheet and Wikipedia’s notation.
In your example g^-1(X) = 1/X.
Otherwise an element-by-element division would give you a vector for the acceptance rate, what could you do with that?
LikeLike
I mean that if you have, say, X = (A,B,C) for three parameters A, B and C, then X’/X means (A’*B’*C’)/(A*B*C). This is because, the determinant of the Jacobian from a transformation from a multivariate Gaussian to a multivariate lognormal turns out to be a product. See https://stats.stackexchange.com/questions/214997/multivariate-log-normal-probabiltiy-density-function-pdf?rq=1
LikeLike
In my previous reply, wherever I wrote “g^-1”, I meant of course “the Jacobian of g^-1”, sorry for the confusion.
So you need the determinant of the Jacobian of g^-1.
LikeLike
Thanks for the follow up and clarification.
Jim
LikeLike
Thanks for thsi guide. I’ve a fair knowledge in R and substantial theory in MCMC. Despite this, however, I have for the past 1 month tried to implement the model in the following paper (“A Bayesian Semi-Parametric Model for Small Area Estimation”, by Donald Malec and Peter Muller) without success. I’ve created a similar (fake) data for purposes of understaning modelling using Dirichlet Process Mixture (DPM) priors.
Any help on how to go about this would be highly apprecaited. I badly need to understand how to code this in R.
LikeLike